Las matrices especiales son aquellas que tienen ciertos tipos de características en particular, a continuación, las describiremos:
- Matriz Identidad: Es una matriz cuadrada en donde cada uno de sus elementos es igual a cero, excepto por su diagonal principal en donde cada uno de sus elementos son iguales a uno, se representa con In.
Matriz Diagonal: Cada uno de sus elementos fuera de la diagonal son iguales a cero, se denota por [D]ij = 0 para todo i≠j. En la matriz diagonal siempre se debe indicar la diagonal y su dimensión, a continuación, observaremos un ejemplo de una matriz diagonal.
A
= diag ((1,2), 2*2)
B = diag ((3,2,5), 3*3) C
= diag ((2,2), 2*3)
Matriz Triangular Superior: Todos los elementos que están por debajo de la diagonal, son iguales a cero, se denota de la siguiente manera [Ts]ij = 0 si i > j. Ejemplo:
Triangular Inferior: todos los elementos que están por encima de la diagonal, son iguales a cero, es decir si aij = 0 para i < j
Matriz Simétrica: Una matriz simétrica es una matriz de orden n con el mismo número de filas y columnas donde su matriz traspuesta es igual a la matriz original, es decir A = AT Ejemplo:
Matriz Transpuesta: La matriz traspuesta de una matriz A se denota por AT y se obtiene cambiando sus filas por columnas (o viceversa). Sea A una matriz de dimensión m*n, denotamos al elemento de la fila i y columna j como A(i,j), siendo i<m y j < n. Entonces, se define la matriz traspuesta de A como la matriz AT de dimensión n*m tal que AT(j,i) = A(i, j), siendo i < m y j < n. En el siguiente ejemplo podemos observar que la primera fila de la matriz A es (1,0,4) y esta fila es la primera columna de su matriz traspuesta.
Matriz ampliada: Es también llamada matriz aumentada, se forma al añadir a una matriz cuadrada otra matriz. La matriz aumentada se emplea para encontrar la matriz inversa y en la resolución de sistemas de ecuaciones lineales. Este es un ejemplo de una matriz aumentada a partir de la matriz (A) aumentada con la matriz (B):


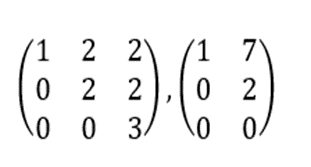








No hay comentarios:
Publicar un comentario